Teaching
Here you will find an overview of the courses
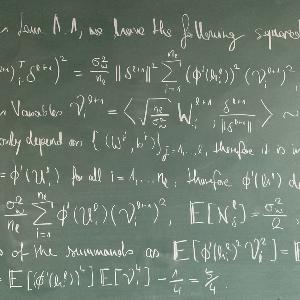
Here you will find an overview of the courses
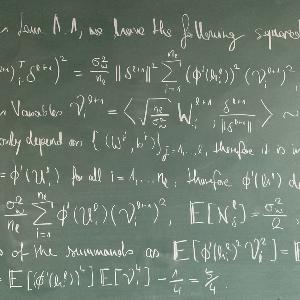
In the winter term 2025, Professor Kutyniok's office hours will take place on Thu 12:30pm - 13:30 pm.
Course Description
(as in WiSe2023/2024)
A modern mathematician needs solid programming and data analysis skills to solve real-world problems in finance, medicine, technology or science. Working with data, solving mathematical problems computationally, and visualizing results are important skills to combine with mathematical knowledge. Therefore, the aim of this course is to provide a link between mathematics and computer science for the mathematics students. We will offer an introduction into Python programming language and its applications to mathematics and data analysis. Specifically, we will focus on packages for scientific computing and linear algebra (NumPy, SciPy), data handling (Pandas), visualisation (Matplotlib) and symbolic computation (SymPy).
Course Description
(as in 2023)
Due to its remarkable success in a wide range of applications, machine learning plays an increasingly prominent role in the intersection of mathematics, statistics, and data science. Consequently, it becomes more and more important to understand and develop theory that supports further advancement in machine learning. This course provides the fundamental concepts and frameworks in machine learning, including PAC learning framework, Rademacher complexity, VC-dimension, empirical risk minimization, support vector machine, kernel methods, and more.
Course Description
(as in WS2023/2024)
Applied Harmonic Analysis is a subarea of Harmonic Analysis and studies efficient representations and the analysis of functions. Methods from this area are today used in a variety of fields ranging from operator theory over partial differential equations up to real-world applications in data science. This makes it not only a very exciting and versatile research area, but also a foundational area of mathematics. The results in this field draw from several topics such as approximation theory, Fourier analysis, functional analysis, and microlocal analysis.
Course Description
(as in 2024)
Signals and images are the most widely used types of data with numerous applications. The area of mathematical signal and image processing aims to develop methods for their acquisition and analysis, which arise from and allow a deep mathematical understanding. Of particular interest in this area are also inverse problems, which aim to recover signals or images from measurements in the sense of inverting the measurement operator. Intriguingly, various of the methods which were developed to solve such problems led in turn to deep mathematical theories, such as wavelet systems in the realm of approximation theory and functional analysis. Finally, a recent development also connects the area of mathematical signal and image processing with artificial intelligence, in particular, deep neural networks.
This lecture will provide an introduction into this exciting and rich research area. Some of the topics, which we will discuss, are:
Course Description
(as in SoSe2023)
Optimization is a fundamental tool for data science and machine learning. From a practical point of view, it is crucial to understand the convergence behavior of the various optimization methods. In light of modern large-scale applications, resource efficient first-order methods are here of particular interest. Relying on the mathematical theory of convex analysis, it is possible to derive rigorous convergence rates for such methods. Moreover, the developed theory often can be transferred to general non-convex problems.
This lecture will provide an introduction into the basic concepts of convex analysis and will show, how the theory can be used to analyze the convergence behavior of first-order methods like gradient descent. In particular, the presented methods will be linked to concrete data science problems. The topics we discuss will encompass:
Course Description
(as in SoSe2023)
Artificial intelligence (AI) is currently changing public life and science in an unprecedented way. One of the central methods used are artificial neural networks, often summarized under the term 'deep learning', that are modeled after the human brain. There is currently intense research from various sides to develop a mathematical foundation of AI, for example to analyze phenomena such as missing robustness, understand the behavior of training algorithms, or explain the decisions of an AI algorithm. Additionally, AI-based methods are increasingly being used in mathematical fields such as (partial) differential equations.
Differential equations are mathematical equations that describe the relationship between a function and its derivatives with respect to one or more independent variables. In other words, a differential equation is an equation that involves the derivatives of a function. Differential equations arise naturally in many areas of science and engineering, and they are used to model a wide range of physical phenomena, including motion, heat transfer, fluid flow, chemical reactions, and many more. They are also applied in many other fields, such as economics, finance, and biology. Based on their properties, differential equations can be classified into several categories, such as order, linearity, and type of coefficients.
Solving differential equations is an important topic in mathematics, and there are many methods for finding solutions to different types of differential equations. These methods include analytical techniques, such as separation of variables and the method of integrating factors, as well as numerical methods, such as Euler's method and the Runge-Kutta method. The runtime of the numerical methods differ from method to method and from equation to equation and is usually expressed in terms of the discretization parameters. The complexity of these numerical schemes increases with the difficulty of the equations they seek to solve, making them computationally expensive. Although methods like the finite element method are quite successful for many classes of partial differntial equations, they require fine-tuning to handle different types of conditions and often suffer from problems like the curse of dimensionality.
In this course, we will present selected topics on deep learning methods for partial differential equations based on selected papers. These methods range from purely data-driven models such as Fourier Neural Operator to purely model-based approaches such as Physics Informed Neural Networks. We will begin by reviewing some terms from the theory of partial differential equations and the theory of deep learning. We will then cover selected topics such as operator learning, physics informed neural networks, neural networks for parametric PDEs, the deep Ritz method, etc.
Course Description
(as in WiSe2023/2024)
Probabilistic methods are a fundamental tool for data science and machine learning. Apart from allowing a deeper understanding of the geometry of high-dimensional spaces (in which data normally lives), they open up resource efficient ways to solve deterministic problems.
This lecture will provide a fundamental probabilistic toolbox for analyzing problems in high dimensions. The topics we discuss will encompass:
Artificial intelligence (AI) is currently changing public life and science in an unprecedented way. Deep artificial neural networks, which mimic the human brain, are one of the central methods here; these are usually summarized under the term "deep learning". If you take a closer look, the class of neural networks is nothing more than a parameterized structured function class, i.e. a highly mathematical object.
Intensive research is currently being carried out, particularly on the mathematical side, to develop a mathematical basis for deep learning, for example to analyze phenomena such as a lack of robustness, to understand the behaviour of training algorithms or to explain the decisions of an AI algorithm. Depending on the problem at hand, a wide variety of mathematical methods are used, from algebraic geometry, functional analysis and stochastics to discrete mathematics such as graph theory and even mathematical logic.
In our seminars offer an introduction to various of these topics. Each presentation will be based on a scientific article, so that the presentations can also be prepared independently of each other. Of course, great attention will be paid to the previous knowledge and interests of the respective participant. At the end of the seminar, each participant will have gained a deep understanding of their own topic as well as a very good overview of this exciting and highly topical field of research. In order to further improve the quality of the presentations and since giving presentations is of central importance for any professional development, we will conduct a short rhetoric training at the beginning.
30.10.2025 - Yan Sholten Recent Frontiers in Trustworthy AI for Large Language Models
13.11.2025 - Laura Kriener Event-based computation and learning for neuromorphic hardware
20.11.2025 - Laurent Jaques Math Colloquium
04.12.2025 - Christoph Hertich Understanding Neural Network Expressivity via Polyhedral Geometry
18.12.2025 - Sophie Jaffard CHANI: Correlation-based Hawkes Aggregation of Neurons with bio-Inspiration
08.01.2026 - Michael Hedderich Technical and Human-Centric Perspectives on Understanding LLM Behavior
22.01.2026 - Vasco Brattka
29.01.2026 - Bernhard Schmitzer