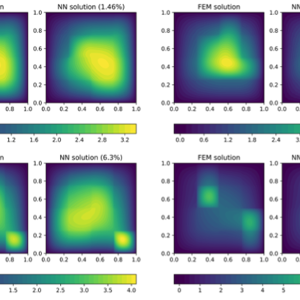
Neural networks and PDEs
Nowadays, advanced computational tools are used to address challenges in partial differential equations (PDEs) and scientific machine learning. Key areas include Physics-Informed Neural Networks (PINNs) for solving PDEs flexibly, Neural Operators for learning solution operators in the infinite-dimensional space, and Symbolic Regression to discover interpretable mathematical relationships from data. These methods aim to combine the rigor of mathematical modeling with the flexibility of modern machine learning to tackle complex problems across science and engineering.